Haversine Search - Finding the Closest Airport to a Given Place

While building Itinerary, we came across an interesting problem that I thought would be worth sharing. In case you have not used Itinerary, it takes in a set of inputs (source, destination, dates, and budget) and then builds a complete itinerary with day-to-day recommendations around food, activities, and accommodations.

Try it out here: Itinerary

In this article, I will be explaining how we solved the challenge of finding the closest airport to any given place on Earth using KD-Trees and the Haversine formula. This might sound complex, but I'll break it down step by step.

The Problem

Itinerary has a feature where it provides direct links to SkyScanner for flights from the source destination to the target destination. Building this link is simple, since we can pass URL paths for both the places, as well as the dates. For example, Skyscanner link for flights from Bengaluru to Delhi from 23rd May to 30th May would look something like this:

https://www.skyscanner.co.in/transport/flights/blr/del/250823/250830

Breaking down the link:

• Source: BLR (IATA Code for Bengaluru Airport)
• Destination: DEL (IATA Code for Delhi Airport)
• From Date: 250823 (23rd May 2025)
• To Date: 250830 (30th May 2025)

Skyscanner uses IATA codes for airports to fetch flights. What is an IATA Code?

An IATA code is a three-letter code assigned by the International Air Transport Association (IATA) to identify airports around the world. These codes are used in ticketing, baggage handling, and flight planning to simplify communication and avoid confusion.

We already take the From and To dates from the user as is, but we cannot get the IATA code for the airport directly from the user, since there is no direct semantic link between the IATA code and the name of a place. Delhi's IATA code might be the first three letters DEL, but this logic does not apply to all airports. For example, London's airport code is LHR (London Heathrow Airport).

Things get even more complex when you consider places that do not have an airport and would need to fetch flights for nearby cities with airports.

So how do we solve this problem of fetching the closest airport to a given place?

Understanding Our Input Data

Let's understand how we are getting the From and To destination as user input. We cannot let the user put any random text for the To and From destination, and hence we are using Google Maps Autocomplete API that provides autocomplete suggestions to the users based on the user input. A sample autocomplete response would look something like this for the input query of "Par":

{
  "predictions": [
    {
      "description": "Paris, France",
      "place_id": "ChIJ24L39Vv0140RbQ9fH3g3X34",
      "matched_segments": [
        {
          "text": "Paris"
        }
      ],
      "place_type": ["city"],
      "structured_formatting": {
        "main_text": "Paris",
        "secondary_text": "France"
      }
    },
    {
      "description": "Paris, Île-de-France, France",
      "place_id": "ChIJ0u3G53f0140R1281912331",
      "matched_segments": [
        {
          "text": "Paris"
        }
      ],
      "place_type": ["administrative_area_level_1"],
      "structured_formatting": {
        "main_text": "Paris",
        "secondary_text": "Île-de-France, France"
      }
    }
  ],
  "status": "OK"
}

If the user selects the first option, the backend receives the place_id of the place, which is a unique identifier of the place in Google Maps. We can use another maps API to get the coordinates of a place ID as follows:

https://maps.googleapis.com/maps/api/place/details/json?place_id=PLACE_ID&key=YOUR_API_KEY

Sample Simplified Response:

{
  "result": {
    "geometry": {
      "location": {
        "lat": 37.7749,
        "lng": -122.4194
      }
    }
  }
}

So now, our problem reduces down to finding the closest airport to a given coordinate.

1. First Approach: Google Maps Nearby Search

Our first approach was to use another maps API that searches for places of a particular type around a given coordinate and radius. It would look something like this:

https://maps.googleapis.com/maps/api/place/nearbysearch/json?location=LAT,LNG&radius=50000&type=airport&key=YOUR_API_KEY

Sample Response:

{
  "results": [
    {
      "name": "San Francisco International Airport",
      "place_id": "ChIJVXealLU_xkcRja_At0z9AGY",
      "geometry": {
        "location": {
          "lat": 37.6213,
          "lng": -122.379
        }
      }
    }
    // more results...
  ]
}

But this has some very obvious problems:

1. No concrete way to tweak the radius parameter. The closest airport to a city (especially in India) might very well be further than 100-200 Kms
2. The API does not return the IATA code. It follows the schema of a generic Google Maps place object. Therefore this API is of no use to us at all.

So what next?

2. The Dataset Approach

When you think about it, there are not a lot of airports in the world. The number is around ~6000 and the list of airports does not get updated very frequently either.

After some browsing and searching, we were able to find a data file of all the airports in the world with the following columns in the dataset:

id,name,city,country,iata,icao,latitude,longitude,altitude,timezone,dst,tz,airport_type,source

We downloaded, and cleaned the data since we only need the following columns:

iata,latitude,longitude

Now the problem is reduced to simply finding the closest coordinate from a list of ~6000 coordinates to a given coordinate.

Sounds simple? Yes.
Is it simple? Not exactly.
How do we do it?

Enter KD Tree and Haversine Search.

3. What is a KD Tree?

A KD-Tree (short for k-dimensional tree) is a data structure used for organizing points in a k-dimensional space. It's a type of binary search tree where each node represents a point in k-dimensional space and partitions the space into two halves based on one of the k dimensions.

Why use a KD Tree?

• Efficient for Range and Nearest Neighbour Queries: The KD-Tree is particularly efficient for problems like range search or nearest neighbour search.
• Recursive Partitioning: The space is recursively divided along one of the k dimensions (e.g., x, y, z for 3D space). Each level of the tree splits along one dimension, alternating between dimensions at each level.
• Balanced Structure: Ideally, a KD-Tree is balanced, meaning each node splits the data in such a way that the left and right subtrees have approximately the same number of points, leading to better performance.

In the context of 2D coordinates, the KD-Tree splits data along the X and Y axes alternately and it would look something like this:

4. What is Haversine Search?

The Haversine formula is used to calculate the great-circle distance between two points on the surface of a sphere (like Earth), given their longitude and latitude. This formula accounts for the spherical shape of the Earth, unlike the simpler Euclidean distance.

Haversine Formula:

The formula to calculate the distance between two points:

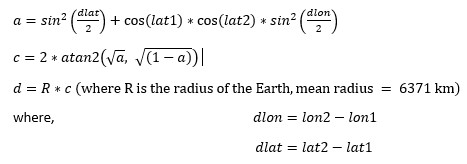
// haversine calculates the Haversine distance between two points in kilometers.
func haversine(lat1, lng1, lat2, lng2 float64) float64 {
	toRad := func(deg float64) float64 {
		return deg * math.Pi / 180.0
	}

	const R = 6371 // Earth radius in km
	dLat := toRad(lat2 - lat1)
	dLng := toRad(lng2 - lng1)
	radLat1 := toRad(lat1)
	radLat2 := toRad(lat2)

	a := math.Sin(dLat/2)*math.Sin(dLat/2) +
		math.Cos(radLat1)*math.Cos(radLat2)*
			math.Sin(dLng/2)*math.Sin(dLng/2)
	c := 2 * math.Atan2(math.Sqrt(a), math.Sqrt(1-a))
	return R * c
}

5. Combining KD-Tree and Haversine Search

By combining KD-Tree for efficient spatial organization with the Haversine formula for calculating distances on a sphere, we can perform efficient nearest neighbor searches in a geospatial context. Here's how they work together:

Step 1: KD-Tree Construction

• When the application starts, the list of coordinates is inserted into the KD-Tree. For each point, the tree structure will allow efficient searching in low-dimensional space (2D for latitude/longitude).
• While constructing the tree, we partition the space using alternating x (longitude) and y (latitude) axes.

Step 2: Search for Nearest Neighbor

• When given a query point (latitude, longitude), the KD-Tree allows us to quickly narrow down the region of interest.
• The query point is compared with the tree nodes, and the search recursively traverses the tree to find the closest points based on the partitions of the space.

Step 3: Distance Calculation (Haversine)

• Once the nearest neighbors are found (i.e., the closest candidates in the KD-Tree), we can then calculate the exact Haversine distance between the query point and the candidate points.

Step 4: Final Closest Point

• After computing Haversine distances for the nearest neighbors found via the KD-Tree, we can determine the closest point.

6. Understanding the Time Complexity

The time complexity of finding the nearest coordinate to a given coordinate depends on a combination of the KD-Tree construction and the nearest neighbor search algorithm, and can also be affected by the use of the Haversine formula to compute distances.

KD-Tree Construction:

• Time Complexity: O(N log N)
  Building a balanced KD-Tree from a set of N points (coordinates) takes O(N log N) time. Each point is inserted into the tree in a way that ensures the tree is balanced, leading to a logarithmic depth for each node.

This is a one-time process and only happens when the backend server starts for the first time.

Nearest Neighbor Search (KD-Tree Traversal):

• Time Complexity: O(log N)
  Once the KD-Tree is built, finding the nearest neighbor to a given query point generally takes O(log N) time in the average case. This is because the KD-Tree partitions the search space, and we can efficiently eliminate large portions of the tree that are far from the query point. The traversal of the tree proceeds in a logarithmic fashion due to the hierarchical structure.

Haversine Distance Calculation:

• Time Complexity: O(1)
  The time complexity for calculating the Haversine distance between two points (latitude and longitude) is constant, i.e., O(1). This is because the Haversine formula involves a fixed number of arithmetic operations (like sine, cosine, and square root), and does not depend on the size of the dataset.

Combined Time Complexity:

1. Building the KD-Tree: O(N log N)
2. Nearest Neighbor Search: O(log N)
3. Distance Calculation: O(1)

Therefore, this makes searching up airports incredibly fast.

7. Is This Premature Optimization?

Now, one can and should argue that searching in a space of ~6000 items should not require implementing a tree data structure and the advantages of using a tree data structure are minuscule and this is a textbook case of premature optimization. That is a very valid argument. However:

1. Performance matters for user experience. We are relying on OpenAI models for a part of the itinerary generation, and it is a painfully slow process by REST standards. The API call to generate the itinerary is a synchronous call with no polling as well, so every millisecond that we can save in this processing, directly affects the user experience.

2. Implementing things is fun. And if we are not having fun, then what is the point?